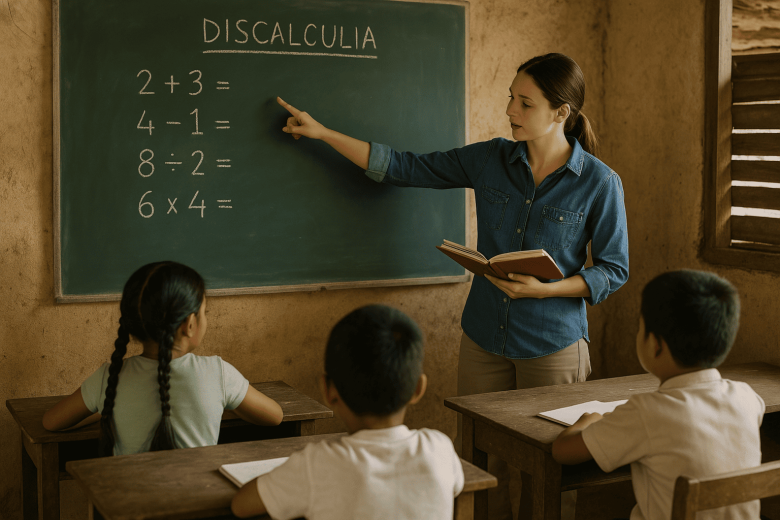O ensino de matemática é um dos maiores desafios enfrentados por educadores em escolas públicas rurais. Dificuldades estruturais, escassez de recursos e a ausência de formação continuada são apenas alguns dos fatores que comprometem o desempenho dos alunos.
Quando se trata de crianças com transtornos de aprendizagem, como a discalculia, a situação se torna ainda mais complexa. O Método Feynman surge como uma alternativa acessível e eficaz para tornar o ensino mais compreensível, prático e inclusivo.
O que é a Discalculia?
A discalculia é um transtorno específico de aprendizagem que afeta a capacidade de compreender e manipular números. Crianças com discalculia apresentam dificuldades significativas em atividades como somar, subtrair, entender proporções e identificar padrões matemáticos. Ao contrário de um baixo desempenho pontual, a discalculia é persistente e exige estratégias pedagógicas diferenciadas.
Principais sintomas:
- Dificuldade com sequências numéricas
- Problemas em compreender o valor posicional
- Incapacidade de estimar quantidades
- Erros frequentes em cálculos simples
A identificação precoce é essencial para que intervenções pedagógicas sejam aplicadas com eficácia, evitando que essas crianças desenvolvam aversão permanente à matemática ou abandonem os estudos por frustração acumulada.
Desafios do Ensino de Matemática em Escolas Públicas Rurais
As escolas rurais enfrentam obstáculos particulares. Além das questões estruturais, como acesso limitado à internet e falta de materiais didáticos, o ambiente muitas vezes não está preparado para atender às necessidades específicas de alunos com transtornos de aprendizagem. Professores acumulam funções, têm pouca formação especializada e enfrentam turmas multisseriadas.
Principais desafios:
- Recursos didáticos escassos
- Alta rotatividade de docentes
- Falta de acompanhamento psicopedagógico
- Dificuldade de engajamento da comunidade escolar
Outro desafio comum é a dificuldade de se trabalhar com metodologias ativas, muitas vezes desconhecidas ou pouco aplicadas nesse contexto, o que torna o ensino mais conteudista e menos significativo para os alunos.
O que é o Método Feynman?
Criado pelo físico Richard Feynman, esse método visa facilitar o aprendizado por meio da simplicidade e da autoexplicação. A ideia central é que, para entender de verdade um conceito, é preciso ser capaz de explicá-lo com palavras simples, como se fosse para uma criança.
Etapas do Método:
- Escolher o conceito a ser estudado
- Explicar com palavras simples, como se ensinasse a outra pessoa
- Revisar os pontos de dúvida, pesquisando e aprendendo mais
- Simplificar e usar analogias para tornar a explicação ainda mais clara
Essas etapas não apenas reforçam o aprendizado, como também desenvolvem a capacidade de comunicação e organização do pensamento. Para crianças com discalculia, o uso da linguagem simples e a associação com experiências concretas facilita significativamente a compreensão de conceitos matemáticos.
Benefícios para Crianças com Discalculia
O Método Feynman estimula a construção ativa do conhecimento. Crianças com discalculia se beneficiam ao transformar conceitos abstratos em linguagem acessível. O processo de “ensinar para aprender” permite que essas crianças desenvolvam maior segurança e compreendam a matemática de forma concreta.
Como ajuda especificamente:
- Incentiva a verbalização dos conceitos matemáticos
- Reduz a ansiedade ao abordar o conteúdo de forma lúdica
- Estimula a memória ao repetir e reorganizar informações
- Promove conexões entre o conteúdo e o cotidiano da criança
Além disso, o uso de analogias, desenhos e recursos visuais torna o processo mais dinâmico e compatível com diferentes estilos de aprendizagem, o que é essencial quando lidamos com dificuldades específicas.
Estratégias para Implementar o Método Feynman em Escolas Rurais
Mesmo com poucos recursos, é possível aplicar o Método Feynman de maneira eficaz. O segredo está na criatividade dos educadores e no uso inteligente dos elementos do cotidiano da criança.
Sugestões práticas:
- Capacitação básica de professores em neuroeducação
- Uso de objetos do dia a dia (feijões, pedras, tampinhas) para representar conceitos matemáticos
- Formação de duplas de ensino (um aluno explica para outro)
- Criação de “diários de aprendizado” com explicações simples
- Registros em áudio ou vídeo para revisão posterior
Outra estratégia é promover “feiras de explicação”, onde os alunos montam estandes e explicam para outros colegas conceitos matemáticos que aprenderam. Essa prática desenvolve não apenas o conhecimento, mas também habilidades de comunicação, cooperação e autoestima.
Exemplo Prático: Ensinando Frações com o Método Feynman
Imagine que o objetivo é ensinar a fração “½”. A criança deve usar um objeto conhecido, como uma banana. Ela parte a banana ao meio e depois explica, com palavras simples, que “meio” é quando algo é dividido em duas partes iguais. Em seguida, desenha, reexplica e mostra outro exemplo com uma folha de papel.
Resultado dessa prática:
- Aprendizado mais efetivo
- Redução de bloqueios emocionais com a matemática
- Participação mais ativa na aula
Essa abordagem também permite que o aluno aprenda com seus erros de forma positiva, reexplicando e reconstruindo o conhecimento até que se sinta seguro com o tema.
Resultados Esperados
A adoção do Método Feynman pode transformar a relação dos alunos com a matemática. Em vez de verem a matéria como um conjunto de regras abstratas, passam a enxergá-la como algo que faz parte da vida. A autoestima melhora, a interação em sala cresce e os resultados também evoluem.
Benefícios coletivos:
- Mais inclusão no processo de aprendizagem
- Fortalecimento da relação entre escola e comunidade
- Aumento do desempenho geral da turma
Resultados como maior frequência escolar, redução da evasão e melhora nas médias de notas têm sido observados em experiências com metodologias ativas semelhantes em diferentes contextos educacionais.
Conclusão
Tornar a matemática acessível é um desafio que exige criatividade e dedicação. Com o Método Feynman, mesmo escolas com poucos recursos podem promover uma aprendizagem significativa, especialmente para crianças com discalculia. O ensino se torna mais humano, personalizado e eficaz, contribuindo para uma educação de qualidade em todos os contextos.
Investir em capacitação de professores, valorizar as vivências locais e dar voz às crianças durante o processo de aprendizagem são passos essenciais para que metodologias como essa se tornem realidade nas escolas mais necessitadas do país.